Model Alignment Process

The alignment of generative models with human feedback has significantly improved the performance of natural language generation tasks. For large language models (LLMs), alignment methods like reinforcement learning from human feedback (RLHF) and direct preference optimization (DPO) have consistently worked better than just supervised fine-tuning (SFT) alone based on current research.

This blog aims to elucidate and differentiate between several of these algorithms. We first discuss traditional RL-based alignment methods and then pivot to non-RL methods like KTO (Kahneman-Tversky Optimization).

🤔 Why align?

TLDR: To prevent LLMs from generating illegal, factually incorrect or redundant responses.

LLMs must generate outputs that resonate with human preferences and are helpful for various tasks in their daily lives. Moreover, we cannot allow LLMs to provide users with recipes for making illegal drugs or bombs.

These models can distinguish between authentic information and fabricated content by aligning LLMs with reality and human preferences, ensuring engaging and reliable outputs.

🤝 RLHF

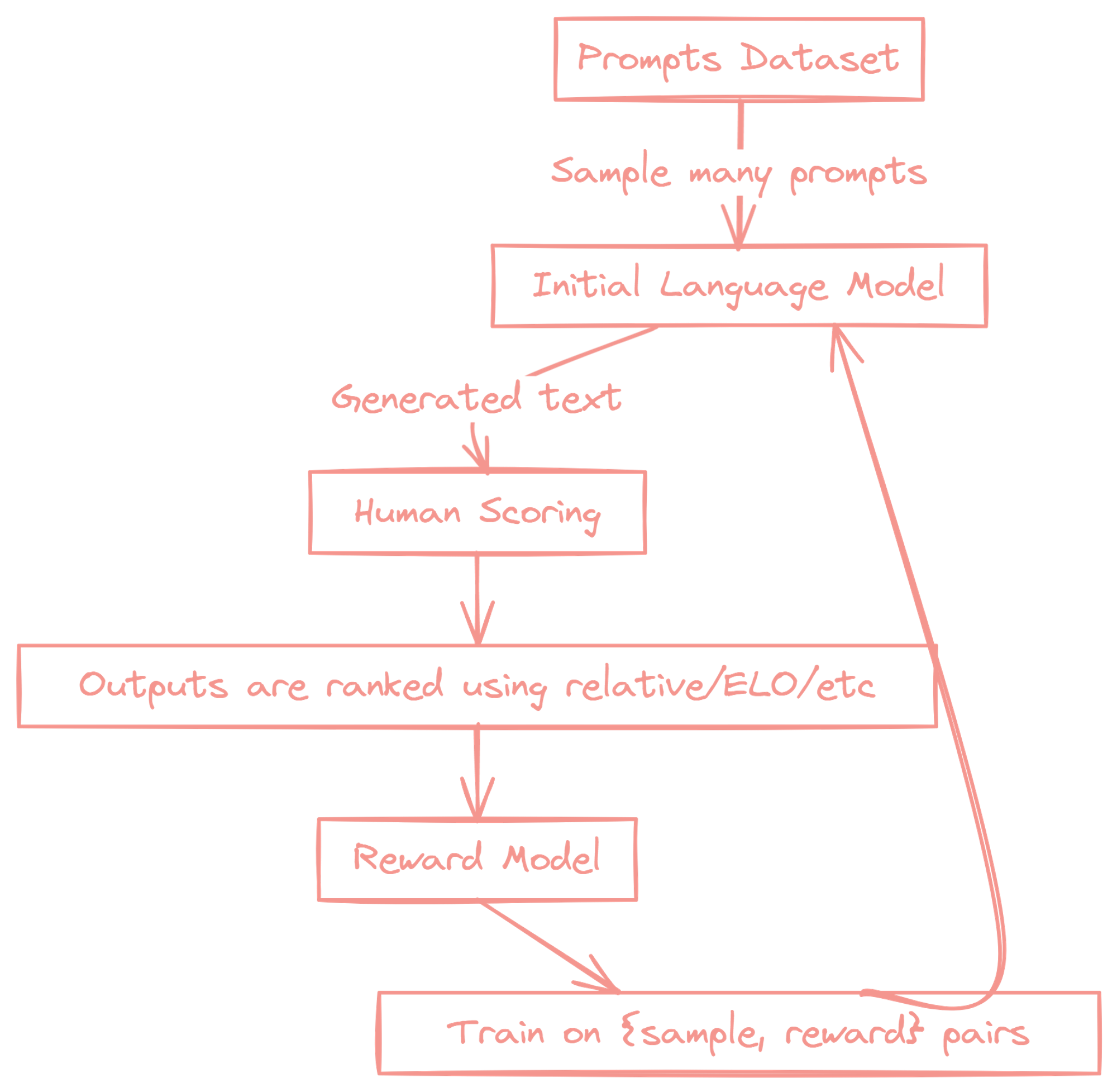
Reinforcement Learning from Human Feedback (RLHF) is what makes ChatGPT so good. Here are the key steps involved in the RLHF process:

1. Data Collection:
   1. Collect a dataset of human-generated examples or demonstrations of the desired behavior or task.
   2. This dataset serves as the foundation for training the AI model.
2. Reward Modeling
   1. Train a reward model using the collected dataset.
   2. The reward model learns to predict the quality or desirability of the AI model's outputs based on human preferences.
   3. It assigns higher rewards to outputs that align with human preferences and lower rewards to those that don't.
   4. Here is an example of Reward Model collection and benchmarking for Reward models.
3. Policy Optimization:
   1. Use reinforcement learning algorithms to optimize the AI model's policy based on the reward model.
   2. The AI model learns to generate outputs that maximize the predicted rewards from the reward model.
   3. This step aims to align the AI model's behavior with human preferences captured by the reward model.
4. Human Feedback Loop:
   1. Collect additional human feedback on the AI model's outputs during training.
   2. Present the model's generated outputs to human evaluators and ask them to provide feedback or ratings.
   3. This feedback is used to further refine the reward model and guide the policy optimization.
5. Iterative Refinement:
   1. Repeat steps 3 and 4 iteratively to continuously improve the AI model's performance.
   2. As more human feedback is collected, the reward model becomes more accurate in capturing human preferences.
   3. The AI model's policy is refined based on the updated reward model, leading to better alignment with human values.
6. Evaluation and Deployment:
   1. Evaluate the trained AI model on held-out test examples to assess its performance and alignment with human preferences.
   2. The model can be deployed for practical use if it meets the desired criteria.
   3. Continuously monitor the model's performance and collect further human feedback for ongoing refinement.

Mathematically, let's break down the equation. This equation below is a representation of an objective function used in Reinforcement Learning with Human Feedback (RLHF):

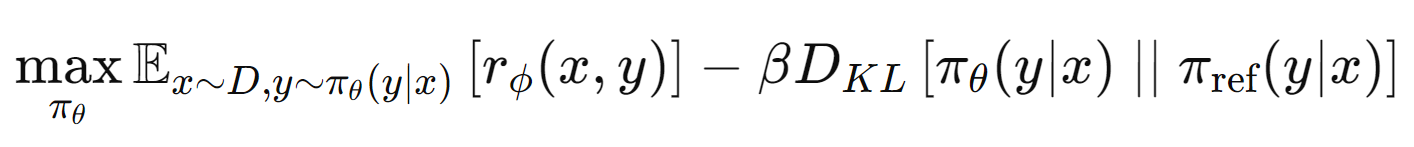
The Kullback-Leibler (KL) divergence, also known as relative entropy, is a statistical measure of how one probability distribution differs from another. It quantifies the difference in information represented by two distributions, where a higher KL divergence indicates greater dissimilarity between the distributions.

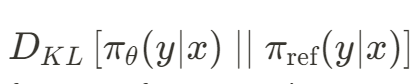
Putting it together, the objective function seeks to find a policy that maximizes the expected reward (as judged by the reward model) for actions \( y \) taken in context \( x \) , while also staying close to a reference policy to maintain behavioral constraints (as controlled by the KL divergence term with coefficient \( \beta \) ).

Note, \( \pi_{\text{ref}} \) is usually the frozen SFT LLM and \( \pi_\theta \) is the active unfrozen LLM in question.

RLHF enables AI models to learn from human feedback and align their behavior with human preferences, making them more reliable, safe, and beneficial for various applications.

Issues with this method:

1. RL is unstable in general.
2. Too many hyper-parameters.
3. Three LLMs to juggle (RM, LLM_ref, LLM_active)

Subscribe to Prem Newsletter

Subscribe

Email sent! Check your inbox to complete your signup.

No spam. Unsubscribe anytime.

TRL Example

TRL by HuggingFace is a full-stack library to fine-tune and align large language models. Here is an example that uses PPOTrainer

# imports
import torch
from transformers import AutoTokenizer
from trl import PPOTrainer, PPOConfig, AutoModelForCausalLMWithValueHead, create_reference_model
from trl.core import respond_to_batch

# get models
model = AutoModelForCausalLMWithValueHead.from_pretrained('gpt2')
model_ref = create_reference_model(model)

tokenizer = AutoTokenizer.from_pretrained('gpt2')
tokenizer.pad_token = tokenizer.eos_token

# initialize trainer
ppo_config = PPOConfig(batch_size=1, mini_batch_size=1)

# encode a query
query_txt = "This morning I went to the "
query_tensor = tokenizer.encode(query_txt, return_tensors="pt")

# get model response
response_tensor  = respond_to_batch(model, query_tensor)

# create a ppo trainer
ppo_trainer = PPOTrainer(ppo_config, model, model_ref, tokenizer)

# define a reward for response
# (this could be any reward such as human feedback or output from another model)
reward = [torch.tensor(1.0)]

# train model for one step with ppo
train_stats = ppo_trainer.step([query_tensor[0]], [response_tensor[0]], reward)

👾 Direct Preference Optimization (DPO)

What if we could avoid employing a reward model and implicitly calculate reward functions? Well, that’s what DPO does.

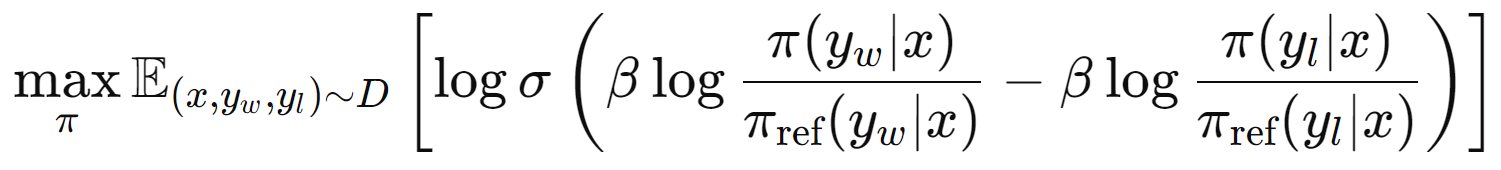
The objective function aims to adjust the policy \( \pi \) so that it is more likely to select responses that are preferred \( (winners, y_w ) \) over those that are not preferred \( (losers, y_l ) \), relative to some reference policy \( \pi_{\text{ref}} \) . By applying the sigmoid function, DPO ensures that the policy is updated smoothly, mitigating the risk of making drastic changes based on individual preferences, which could result in unstable learning.

Here is a CLI example using TRL: trl dpo --model_name_or_path facebook/opt-125m --output_dir trl-hh-rlhf --dataset_name trl-internal-testing/hh-rlhf-trl-style

Refer to the CLI documentation for more details.

☝ Identity Preference Optimization (IPO)

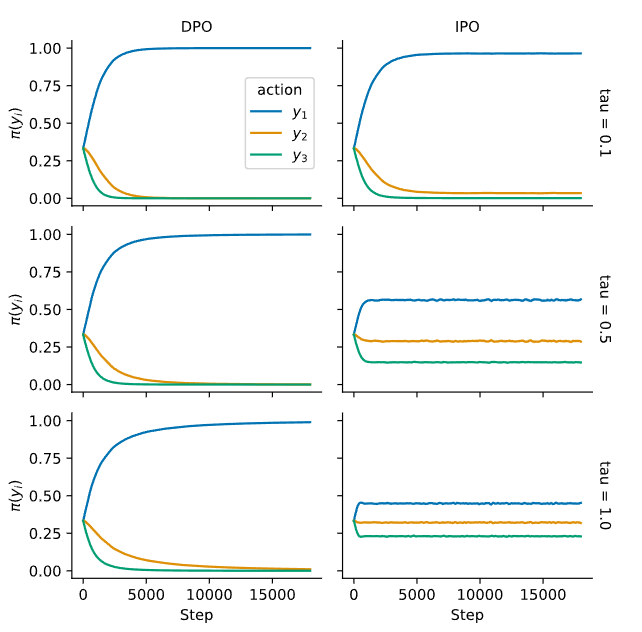
While RLHF and DPO perform well at aligning LLMs, they are far from optimal, given the datasets used for training. DPO is prone to overfitting because it may concentrate too much on the exact outcomes it has seen, leading to a policy that can't generalize well to new situations. Researchers at Google DeepMind introduced Identity Preference Optimisation (IPO), which adds a regularisation term to the DPO loss and enables one to train models to convergence without requiring tricks like early stopping. For a more in-depth explanation of this, refer to this blog.

👀 Do we always need pairs? Enter KTO!

Alignment methods expect feedback in the form of preferences (e.g., Output A is better than B for input X). Utilizing human annotation efforts for this feedback quickly gets very expensive, and can also result in conflicting data. Humans themselves rate subjectively and thus extensive efforts are needed to define how Output A is quantitatively better than Output B.

Kahneman-Tversky Optimization (KTO) draws from the human value function proposed by Kahneman and Tversky in prospect theory. The human value function captures how people perceive gains and losses relative to a reference point, with two key characteristics:

1. Loss Aversion: People feel the sting of losses more intensely than the joy of equivalent gains.
2. Diminishing Sensitivity: The perceived difference between, say, $100 and $200 is more significant than between $1100 and $1200, even though both intervals are $100 apart.

The function is typically concave for gains (reflecting diminishing sensitivity) and convex for losses (reflecting loss aversion), and due to loss aversion, steeper for losses than for gains.

Translating this into KTO for LLMs, the objective function might look something like this: \( h(x, y; \beta) = \sigma(\beta (r(x, y) - z_{\text{ref}})) \)

• \( h \) is the utility based on the output y given input \( x \) .
• \( \sigma \) is a logistic function that models the non-linear perception of utility.
• \( r(x, y) \) is a measure of the output's quality, akin to a reward in RLHF.
• \( \beta \) is a scaling factor related to sensitivity.
• \( z_{\text{ref}} \) is the reference point, which could be the average reward or some baseline measure.

In KTO, the loss function is designed to reflect these human decision-making behaviors: \( L_{KTO}(\pi_\theta, \pi_{\text{ref}}) = \mathbb{E}_{x,y \sim D} \left[ w(y) (1 - \hat{h}(x, y; \beta)) \right] \)

Here, \( w(y) \) is a weighting function that might implement loss aversion by assigning greater weight to avoid losses (undesirable outcomes) compared to achieving gains (desirable outcomes).

Now, compared to DPO, KTO is inherently less prone to overfitting because it does not only rely on preference pairs. It does not aggressively maximize the likelihood of a preference but rather balances the outcomes around a reference point, thus avoiding extreme policies that DPO might settle on due to noisy or limited data.

As for RLHF, while it incorporates a reward function learned from human feedback, it may not inherently account for human psychological biases such as loss aversion or diminishing sensitivity. KTO, by design, includes these biases directly into the optimization process. Therefore, KTO has the potential to create policies that not only align with human preferences but do so in a way that's more reflective of how humans actually make decisions, potentially leading to more nuanced and human-like behavior in LLMs.

Here is some TRL test code for KTOTrainer:

import torch
from datasets import Dataset
from transformers import AutoModelForCausalLM, AutoTokenizer
from trl import KTOConfig, KTOTrainer

def train_with_kto():
    model_id = "your-model-id"
    model = AutoModelForCausalLM.from_pretrained(model_id)
    ref_model = AutoModelForCausalLM.from_pretrained(model_id)
    tokenizer = AutoTokenizer.from_pretrained(model_id)
    tokenizer.pad_token = tokenizer.eos_token

    training_args = KTOConfig(
        output_dir="your-output-dir",
        per_device_train_batch_size=2,
        max_steps=3,
        remove_unused_columns=False,
        gradient_accumulation_steps=1,
        learning_rate=9e-1,
        evaluation_strategy="steps",
        beta=0.1,
    )

    # Prepare your dataset
    dummy_dataset = Dataset.from_dict({
        "prompt": ["Your", "prompt", "texts"],
        "completion": ["Your", "completion", "texts"],
        "label": [True, False, True],  # Optional
    })

    trainer = KTOTrainer(
        model=model,
        ref_model=ref_model,
        args=training_args,
        tokenizer=tokenizer,
        train_dataset=dummy_dataset,
        eval_dataset=dummy_dataset,  # Optional
    )

    trainer.train()

🌀 Self-Play fIne-tuNing (SPIN)

Self-Play Fine-Tuning (SPIN) is a method designed to enhance the capabilities of Large Language Models (LLMs) through a unique self-improvement process that doesn't rely on additional human-annotated data. Here's a breakdown of how SPIN operates, as outlined in the algorithm:

1. Inputs: The method starts with a dataset consisting of pairs \( (x_i, y_i) \) from Supervised Fine-Tuning (SFT), an initially parameterized LLM \( (p_{\theta_0}) \), and a set number of iterations T.
2. Iteration Process: The algorithm enters a loop that runs for T iterations, where t represents the current iteration.
   • Synthetic Data Generation: For each data pair \( (x_i, y_i) \) in the dataset, the model generates a synthetic response \( y'_i \) using the current version of the LLM \( (p_{\theta_t}) \). This process is akin to the LLM 'playing' against itself, where it tries to generate responses that mimic human ones.
   • Model Updating: The parameter \( \theta \) of the LLM is updated by minimizing a loss function. This loss function is constructed to evaluate two main aspects:
     • The log ratio between the probability of the real response \( y_i \) given \( x_i \) under the new model parameters \( \theta \), and its probability under the current parameters \( \theta_t \).
     • The log ratio for the synthetic response \( y'_i \) under the same conditions.
   • The loss function \( (\ell) \) is applied to these log ratios, weighted by a regularization parameter $\lambda$, and summed over all data pairs. This process nudges the model towards generating responses that are more aligned with human responses and distinguishing them from its previous synthetic outputs.
3. Output: After T iterations, the process outputs the updated model parameters \( \theta_T \), representing the fine-tuned LLM.

The essence of SPIN is its innovative use of synthetic data and self-play to refine the model's ability to generate human-like responses. By iteratively generating responses and training the model to distinguish between its outputs and the actual human responses, SPIN progressively improves the model's performance. This approach offers a promising avenue for enhancing LLMs without the extensive need for new human-labeled data, making the fine-tuning process more efficient and less resource-intensive.

📈 Results

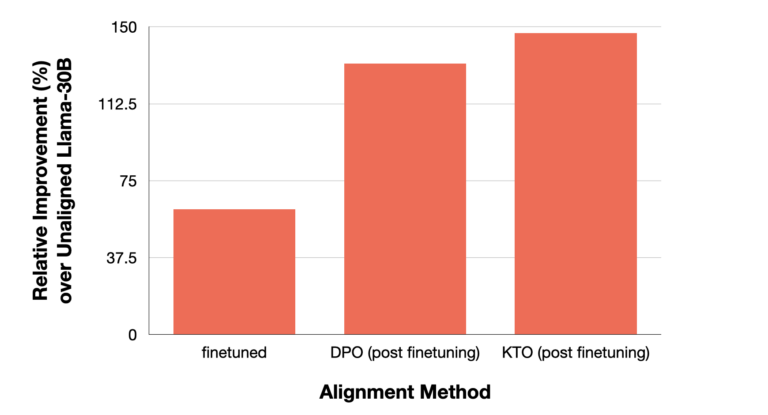
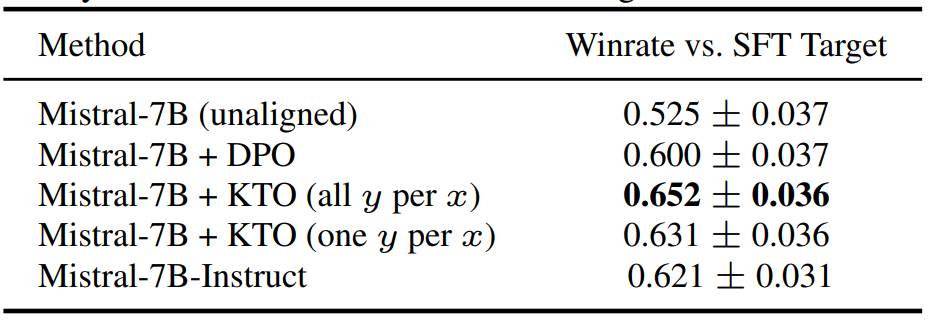
We note from the KTO paper the performance of various alignment algorithms on the Mistral-7B LLM trained on the OpenAssistant dataset (oasst). Note that all y per x / one y per x situations refer to the KTO’s settings (since it doesn’t need paired responses). We observe that compared to the unaligned LLM, KTO even with less number of responses (y) achieves higher win rate. We also note that the instruction-tuned Instruct version also obtained a higher win rate compared to the unaligned and DPO. The rates are provided with a 90 percent confidence interval.

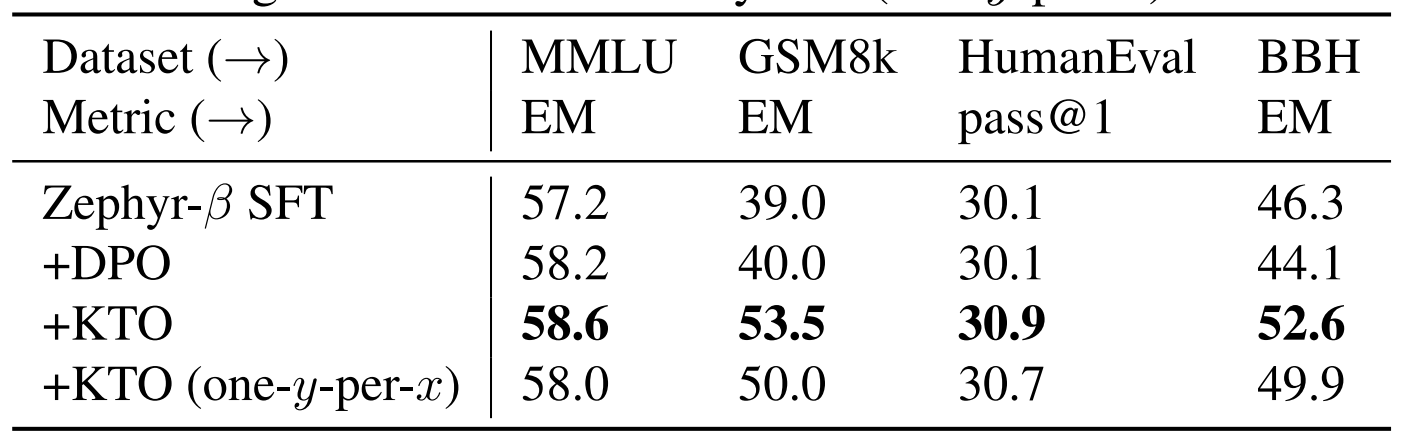
A similar eval test is applied on a derivative of Mistral, named as the Zephyr series by Huggingface. We note that across various static benchmark testing, Zelphyr-Beta (trained on UltraFeedback dataset) aligned via KTO scores higher than mere SFT (with or without DPO). BBH stands for BigBench-Hard.

For more info on static benchmarking of LLMs, head over to our LLM evaluation series.

📜 Resources

• HF blog on Preference Tuning
• Medium blog on KTO
• Reward Bench
• ORPO: Monolithic Preference Optimization without Reference Model
• Preference Ranking Optimization for Human Alignment
• Human Aligned Loss Objectives
• Self-Play Fine-Tuning Converts Weak Language Models to Strong Language Models
• Aligning Large Language Models with Human: A Survey
• Large Language Model Alignment: A Survey
• Blog on SPIN
• UltraFeedback Dataset
• Lewis Tunstall talk on DPO
• ZEPHYR: DIRECT DISTILLATION OF LM ALIGNMENT
• RLHF paper by Ouyang et al (Openai)
• TRL framework for alignment
• KTO: Model Alignment as Prospect Theoretic Optimization
• Comparing Preference Alignment Algorithms
• A General Theoretical Paradigm to Understand Learning from Human Preferences